在设计中,我们往往仅判断元件本身的简单特性,而忽略了元件更复杂的,寄生参数等特性。这往往会导致我们在实验室环境下能够达到要求的板子在更复杂的环境下(不同温度、湿度)等条件下跑不起来。同时忽略了一些信号的频域特性等条件,这期间可能会造成 信号失真 、 无法达到预期要求 等问题。在这篇文章会对基础元器件的隐含特性进行分析。
基本科普 - 阻抗
简单了解
在我刚刚入门电子电路时,常常在教授、工程师、做信号的学长口中听到 “阻抗” 两个字,但好像教科书对这个特性讲的并没有那么通俗易懂。往往是许多人碰到坑、出过错之后才知道这意味着什么。
简单来说,当电路只有直流成分时,我们遇到对电流起到阻碍作用的主要是电阻。而对交流信号时,你的电容、电感等元件也会对电流进行一定的阻碍作用。这个阻碍作用并非是某一个特定的值,而是一个根据信号频率产生不同抗性的特性。
例如我们都知道电容阻碍直流信号,通交流信号。我们不妨看看他的理想阻抗表达式。
$$ R_c = \frac 1 {j \omega C} $$这等价于
$$ R_c = \frac 1 {j 2 \pi f C} $$其中 j 为复数,我们通常用复数来对电容的阻抗进行表达。因为对于这个式子而言,如果我们主要考虑他的频率特性,可以这么写:
$$ R_c = 0 - j\frac 1 {2 \pi C} * \frac 1 f $$对于这个式子,我们可以发现 0 就是作为他实部的电阻,也就是常态下的电阻(无论何时 电路成分为何 都不影响的阻值)。这个就是他常态下的电阻。而右侧他的虚部就代表着他的电抗,表示对能量的储存特性。对于任意的 $ Z = R + jX $,R都代表了电阻部分,X代表了他的电抗。当 X > 0 说明他是感抗 , X < 0 说明他是容抗。
举个例子
根据复变函数相关知识,我们可以将 $ Z = 3 + j4 $ 作为例子,通过欧拉公式将他转换为 $ Z = |R| e^{j \theta} $, 其中:
$ |R| = \sqrt{3^2 + 4^2} = 5$
$ \theta = \arctan{4/3} \approx 54.3$
我们就可以知道,这个电路的阻抗为 5,相位感性滞后约 54.3 °。
也就是说 阻抗 = 电阻(实部) + 电抗(虚部)
推导
同样的,对于刚才我们推导出的阻抗与频率相关的公式。我们可以很轻易地推导出。请注意: ( $ \arctan{\infty} = \frac \pi 2 $)
$$ R_c = |\frac 1 {2\pi C} * \frac 1 f| e^{\frac {j\pi} 2} $$我们肉眼可见,电路中左侧为常数。当信号为理想DC (0Hz) 时,$ R_c = \infty $ ,阻抗无穷大,自然就隔断直流了。
电感的理想公式为 : $ R_l = j\omega L $ 你也可以试着推一下他的"隔交通直"特性!
电容特性
理论层面
电容是电路设计中最常见的元件之一,他的等效特性图可以参考下面。
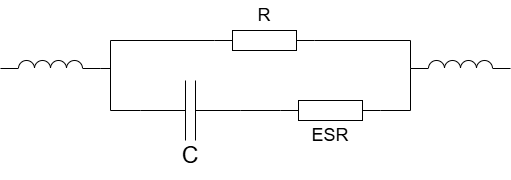
他的参数包含以下:
L : L1 + L2 两个引线电感串联之和
R : 绝缘阻抗 R , 为外加直流电压时对应的漏电流所算出的等效阻抗
ESR : 为低阻阻抗,由于电容的 “隔直流,通交流”特性,交流会选择 较小阻抗的 C->ESR 通路
C : 容值
那么我们认为这个电容的容抗是 $R_c$
$$ R_c = ESR + j \omega L + \frac 1 {jωC} $$经过化简就能得到
$$ R_c = ESR + j(\omega L - \frac 1 {\omega C}) $$还是通过欧拉公式,我们就轻松的得到了他的阻频特性:
$$ R_c = |R_c|e^{j\theta} $$其中 $ |R_c| = \sqrt{{ESR}^2 + (\omega L - \frac 1 {\omega C})^2} $
$ \theta = \arctan(\frac {\omega L - \frac 1 {\omega C}} {ESR}) $
我们考虑到 $ \omega L = \frac 1 {\omega C} $ ,此时 $ |R_c|_{min} = ESR $, 此时带入就能够得到 $ f_0 = \frac 1 {2\pi \sqrt{LC}} $ ,这里 $ f_0 $ 称之为自谐阵频率。
我们电容取100 uF,寄生电感取20 nH,ESR取0.1Ω的典型值,通过改变f的值,得到了如下曲线。
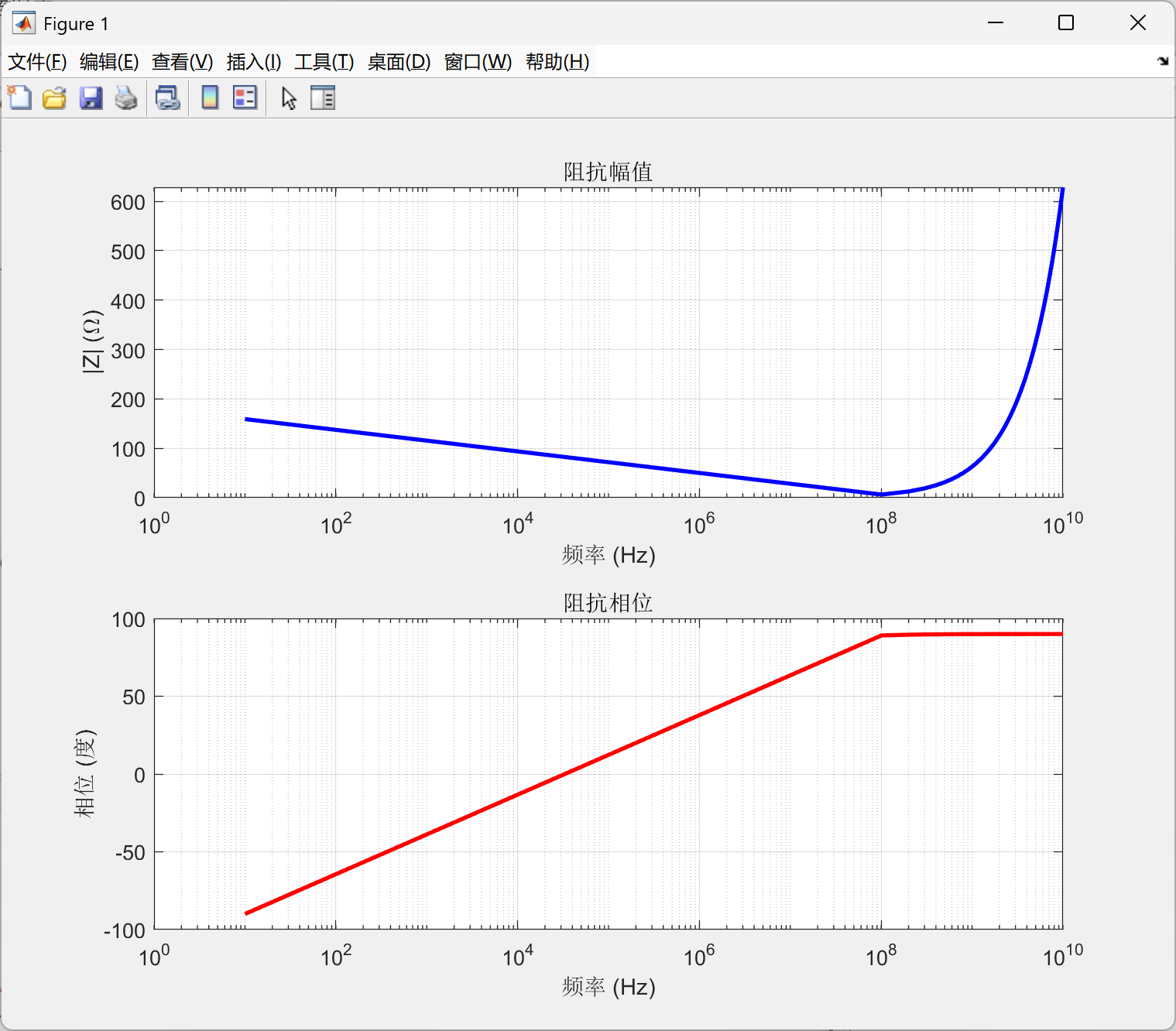
可以发现在f = 100MHz时,他的阻抗最小,而后的信号阻抗将大大增加。也就是说即使这么一个小小的电容。它的对信号的影响仍然不可忽视。同时根据虚部发现,以 10^5Hz 为基准 在低频时电容行为为主,阻抗相位为负。高频时寄生电感起到了大作用,将会使电路偏感性。
应用层面
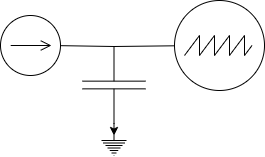
就像这样一个电路,一个信号用于传输,同时向地接了一个电容。假如我们需要传输的是 1Ghz的交流信号,那么就可以将上文计算的电容接在这个位置。由于10^10Mhz之前阻抗较低,这样我们不需要的低频成分就会被滤掉到GND了。同样的,我们可以根据自己需要的滤波成分更改这颗电容的容值。
导线特性
导线在要求不严格的情况下其实是可以忽略的,但在信号大电流、高频 或是 弱信号等状态下,导线的状态就不能忽视了。
趋肤效应

当信号频率较高,电流将趋近与导线表面。根据电阻计算公式:
$$ R = \rho \frac L S $$我们可以知道,当表面积减小,将会导致电阻值增加。
同时这也意味着不同频率的信号在同一条线路上所承受的阻抗也不相同。
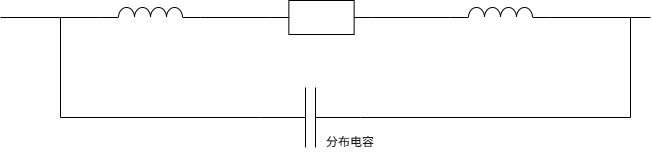
高频模型
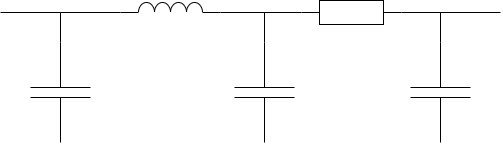
高频情况下,导线可以简化成这样一个模型。也就是说,任何一个导线都是一个 感、容、阻 的集合。
电阻特性
温度特性
我们要参考的主要是电阻的温度系数,这普遍存在于datasheet中,其中以ppm作为主要单位,作为与常温(25°C)差值 每相差1度所造成的误差设为1ppm 一般:
$$ 1ppm = \frac 1 {10^6} $$例如,一个电阻的温度系数为1ppm,其阻值 1MΩ ,则温度相对于标称温度变化1度时,其阻值变化为:
$$ \varDelta R = 1MΩ * 1°C * \frac 1 {10^6} * \frac 1 {°C} = 1 Ω $$高频特性
高频时电阻的等效电路如下: